Dica 1: Como encontrar a altura de um prisma quadrangular
Dica 1: Como encontrar a altura de um prisma quadrangular
Um prisma é uma figura volumétrica composta porum número de faces laterais rectangulares e duas bases paralelas entre si. As bases podem assumir a forma de qualquer polígono, incluindo um quadrilátero. A altura desta figura é o segmento, perpendicular às bases, entre os planos em que se encontram. Seu comprimento no caso geral é determinado pelo ângulo de inclinação das faces laterais às bases prismas.

Instruções
1
Se as condições do problema é dado volume (V) do espaço delimitado pelos bordos prismas, e a área de sua (s) base (s), para calcularaltura (H), use uma fórmula comum aos prismas com uma base de qualquer forma geométrica. Divida o volume pela área base: H = V / s. Por exemplo, com um volume de 1200 cm³ e uma área de base de 150 cm², a altura prismas deve ser igual a 1200/150 = 8 cm.
2
Se o quadrilátero que se encontra na base prismas, tem a forma de qualquer figura correta, em vez da área nos cálculos, você pode usar os comprimentos das bordas prismas. Por exemplo, com uma base quadrada, a área emfórmula do passo anterior, substitua o segundo grau do comprimento da sua aresta (a): H = V / a². E no caso de um retângulo na mesma fórmula, substitua o produto dos comprimentos de duas arestas adjacentes da base (a e b): H = V / (a * b).
3
Para calcular a altura (H) de um quadrilátero regular prismas Pode ser suficiente conhecer a área totalsuperfície (S) e o comprimento de uma borda da base (a). Uma vez que a área total consiste em áreas de duas bases e quatro faces laterais, e em tal poliedro a base é um quadrado, a área de uma superfície lateral deve ser igual a (S-a²) / 4. Este rosto tem duas arestas comuns com bases quadradas de tamanho conhecido, para calcular o comprimento da outra borda, divida a área obtida ao lado do quadrado: (S-a²) / (4 * a). Como o prisma em questão é rectangular, a borda do comprimento calculado por você é adjacente às bases em um ângulo de 90 °; coincide com a altura do poliedro: H = (S-a²) / (4 * a).
4
No prisma quadrangular correto paraO cálculo da altura (H) é suficiente para conhecer o comprimento da diagonal (L) e uma borda da base (a). Considere o triângulo formado por esta diagonal, a diagonal da base quadrada e uma das costelas laterais. A borda aqui é uma quantidade desconhecida que coincide com a altura desejada, e a diagonal do quadrado, com base no teorema de Pitágoras, é igual ao produto do lado da raiz dos dois. De acordo com o mesmo teorema, expresse o valor necessário (cathet) através dos comprimentos da diagonal prismas (hipotenusa) e diagonais de base (segunda etapa): H = √ (L²- (a * V2) ²) = √ (L²-2 * a²).
Dica 2: como fazer um prisma
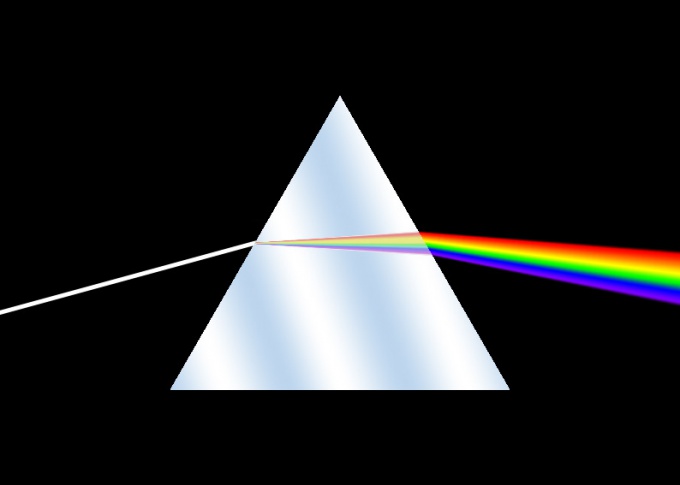
Um prisma é um dispositivo que compartilha um padrãoleve em cores individuais: vermelho, laranja, amarelo, verde, azul, azul, roxo. É um objeto translúcido, com uma superfície plana que refracta ondas de luz de acordo com seus comprimentos e, graças a isso, você pode ver a luz em cores diferentes. Make prisma você mesmo com bastante facilidade.
Você precisará
- Duas folhas de papel
- Foil
- Vidro
- Disco compacto
- Mesa de café
- Lanterna
- Pin
- Água
Instruções
1
O prisma pode ser feito a partir de um copo simples. Encha o copo com água um pouco mais da metade. Coloque o copo na borda da mesa de café para que quase metade do fundo do vidro seja suspenso no ar. Ao mesmo tempo, certifique-se de que o vidro é estável na mesa.
2
Coloque duas folhas de papel uma a uma ao lado da mesa de café. Ligue a lanterna e brilha a luz através do vidro, de modo que cai sobre o papel.
3
Ajuste a posição da lanterna e do papel até ver um arco-íris nas folhas - de modo que seu raio de luz se decompõe em espectros.
Dica 3: Como encontrar a borda de uma pirâmide quadrilateral
A pirâmide quadrangular é um pentaedro comuma base quadrilateral e uma superfície lateral de quatro faces triangulares. As bordas laterais do poliedro se cruzam em um ponto - o topo da pirâmide.

Instruções
1
Uma pirâmide quadrangular pode ser correta,retangular ou arbitrária. Uma pirâmide regular tem um quadrilátero regular em sua base, e seu ápice é projetado para o centro da base. A distância do topo da pirâmide à sua base é chamada altura da pirâmide. As faces laterais da pirâmide regular são triângulos isósceles e todas as bordas são iguais.
2
Na base da pirâmide quadrangular regularpode ser quadrado ou retangular. A altura H de tal pirâmide é projetada até o ponto de interseção das diagonais da base. No quadrado e no retângulo, as diagonais d são as mesmas. Todas as bordas laterais L da pirâmide com base quadrada ou retangular são iguais entre si.
3
Para encontrar a borda da pirâmide, considereum triângulo com lados: hipotenusa - a borda G necessário, as pernas - a altura H da pirâmide, e metade do d diagonal de uma base. Calcular a borda pelo teorema de Pitágoras: quadrado da hipotenusa é igual à soma dos quadrados das pernas: L² = A² + (d / 2) ². Em uma pirâmide com um losango ou de um paralelogramo nas bordas opostas de base são iguais e são determinados pelas fórmulas: L₁² = A² + (d₁ / 2) 'e L₂² = A² + (d₂ / 2) m², onde d₁ e d₂ - base de diagonal.
4
Na pirâmide quadrangular retangular de suaO vértice é projetado em um dos vértices da base, os planos de duas das quatro faces laterais são perpendiculares ao plano da base. Uma das bordas de tal pirâmide coincide com sua altura H, e as duas faces laterais são triângulos retangulares. Considere estes triângulos retangulares: nelas uma das pernas é a borda da pirâmide, coincidindo com a altura H, as segundas pernas são os lados da base aeb, e a hipotenusa são as bordas desconhecidas da pirâmide L1 e L </ s>. Portanto, pelo teorema de Pitágoras, encontre as duas bordas da pirâmide como hipotenuses de triângulos retangulares: L₁² = H² + a² e L²² = H² + b².
5
A quarta vantagem restante LNpirâmide rectangular obter o teorema de Pitágoras como a hipotenusa de um triângulo rectângulo com as pernas e H d, em que d - base de diagonal extraídas da aresta de base que coincide com a altura H da pirâmide para as extremidades inferiores do L₃ título: L₃² = A² + d².
6
Em uma pirâmide arbitrária, seu vértice é projetado emponto aleatório na parte inferior. Para encontrar as bordas de uma tal pirâmide, considere sucessivamente cada um dos triângulos retangulares em que a hipotenusa é a borda desejada, uma das pernas é a altura da pirâmide e a segunda é o segmento que liga o vértice correspondente da base à base da altura. Para encontrar os valores desses segmentos, é necessário considerar os triângulos formados na base quando o ponto de projeção do vértice da pirâmide e os cantos do quadrilátero são unidos.







