Dica 1: Como encontrar o raio de curvatura da trajetória
Dica 1: Como encontrar o raio de curvatura da trajetória
Ao considerar o movimento dos corpos, uma série decaracterizando as quantidades, por exemplo aceleração tangencial e normal (centrípeta), velocidade e também a curvatura da trajetória. O raio de curvatura é um conceito geométrico que indica o raio do círculo R ao longo do qual o corpo se move. Este parâmetro pode ser encontrado a partir das fórmulas correspondentes usando a trajetória de movimento especificada.

Instruções
1
As tarefas mais comuns são determinaro raio de curvatura da trajetória do vôo do corpo abandonado em um determinado intervalo de tempo. A trajetória do movimento neste caso é descrita pelas equações nos eixos de coordenadas: x = f (t), y = f (t), onde t é o tempo em que é necessário encontrar o raio. O cálculo será baseado na aplicação da fórmula e = V² / R. Aqui, o raio R é revelado a partir da proporção da aceleração normal e da velocidade instantânea V do movimento do corpo. Tendo aprendido esses dados, você pode encontrar facilmente o componente desejado R.
2
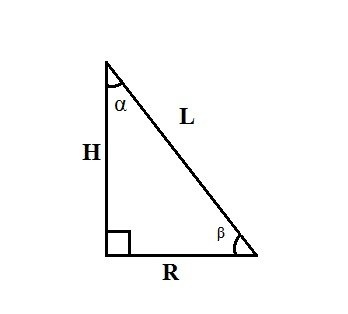
Calcule as projeções da velocidade do corpo nos eixos (OX, OY). O significado matemático da velocidade é a primeira derivada da equação do movimento. Portanto, eles são facilmente encontrados tomando a derivada das equações dadas: Vx = x ", Vy = y". Ao examinar o mapeamento geométrico de dados de projeção no sistema de coordenadas, é claro que são as pernas de um triângulo direito. E a hipotenusa nele - a velocidade instantânea desejada. Com isso, calcule a velocidade instantânea V pelo teorema de Pitágoras: V = √ (Vx² + Vy²). Substituindo na expressão um valor de tempo conhecido, encontre o valor numérico de V.
3
O módulo de aceleração normal também é fácildetermine considerando outro triângulo retangular formado pelo módulo de aceleração absoluta a e pela aceleração tangencial do corpo ak. E aqui a aceleração normal é uma perna e é calculada da seguinte forma: аn = √ (а² - ак²). Para encontrar a aceleração tangencial, diferenciar a equação de velocidade instantânea pelo tempo: ak = | dV / dt |. Calcule a mesma aceleração a partir de suas projeções no eixo, semelhante ao achado da velocidade instantânea. Somente para este propósito, tire das equações de movimento determinadas as derivadas da segunda ordem: ax = x ", ay = y". O módulo de aceleração é a = √ (ax2 + ay2). Substituindo todos os valores encontrados, determine o valor numérico da aceleração normal an = √ (а² - ак²).
4
Expresse a fórmula e = V2 / R a variável requerida do raio de curvatura da trajetória: R = V² / an. Substitua os valores numéricos de velocidade e aceleração, calcule o raio.
Dica 2: Como encontrar o raio da curvatura
Curvatura é um conceito emprestado degeometria diferencial. É o nome coletivo de toda uma série de características quantitativas (vetor, escalar, tensor). A curvatura indica o desvio do "objeto" geométrico, que pode ser uma superfície, uma curva e um espaço riemanniano, a partir de outros objetos "planos" conhecidos (plano, linha, espaço euclidiano, etc.).

Instruções
1
Normalmente, a curvatura é determinada separadamente parade cada ponto desejado em um determinado "objeto" e denotá-lo como o valor de segunda ordem da expressão diferencial. Para objetos com suavidade reduzida, a curvatura também pode ser determinada no sentido integral. Como regra geral, se em todos os pontos curvatura a identidade é zero, então isso implica uma coincidência local do "objeto" dado com o objeto "plano".
2
Digamos que você precisa fazer uma lente plano-convexa. Você só sabe que a força óptica é de 5 dpt. Como encontrar raio curvatura superfície convexa desta lente.Lembre-se da equação: D = 1 / fD é a força ótica (lentes), f é o comprimento focal Escreva a equação: 1 / f = (n-1) * (1 / r1 + 1 / r2) n é o índice de refracção (desse tipo material) r1 - raio lentes de um lado - por outro lado
3
Simplifique a expressão: uma vez que a lente é plano-convexa, é raio com um dos lados tenderá ao infinito, então 1, dividido pelo infinito, tenderá a zero. Você deve obter esta expressão simplificada: 1 / f = (n-1) * 1 / r2
4
Como você conhece o poder óptico de uma lente, descubra a distância focal: D = 1 / f1 / f = 5 dptf = 1/5 dptf = 0,2 m
5
Dada a tarefa, faça uma lente de vidro. Lembre-se de que o vidro tem um índice de refração de 1,5, então a expressão deve ser assim: (1,5 - 1) * 1 / r2 = 0,2 m0,5 * 1 / r2 = 0,2 m
6
Divida todas as partes desta expressão em 0,5. Você deve obter: 1 / r2 = 0,4 mr2 = 1 / 0,4 mr2 = 2,5 m Escreva o resultado: D. Você obterá uma lente plana-convexa raio curvatura 2,5 metros.
Dica 3: como encontrar o raio
Se for um polígono é possível construircircunferência inscrita e circunscrita, a área desse polígono é menor que a circunferência circunscrita, mas maior que a área do círculo inscrito. Para alguns polígonos, as fórmulas são conhecidas por encontrar do raio círculos inscritos e circunscritos.

Instruções
1
Inscrito em um polígono é um círculo tocando em todos os lados do polígono. Para um triângulo, a fórmula do raio círculo inscrito: r = ((p-a) (p-b) (p-c) / p) ^ 1/2, onde p é o semiperímetro; a, b, c são os lados do triângulo. Para um triângulo regular, a fórmula é simplificada: r = a / (2 * 3 ^ 1/2), e a é o lado do triângulo.
2
O polígono descrito em torno dissoUm círculo em que se encontram todos os vértices do polígono. Para um triângulo, o raio do círculo circunscrito é encontrado pela fórmula: R = abc / (4 (p (p-a) (p-b) (p-c)) ^ 1/2), onde p é o meioperímetro; a, b, c são os lados do triângulo. Para um triângulo regular, a fórmula é mais simples: R = a / 3 ^ 1/2.
3
Para os polígonos, nem sempre é possível descobrira razão dos raios das circunferências inscritas e circunscritas e os comprimentos dos lados. Muitas vezes, ele é limitado a construir esses círculos em torno de um polígono e, em seguida, uma medida física do raio círculos com a ajuda de instrumentos de medição ouespaço vetorial. Para construir a circuncisão de um polígono convexo, construa bisecetas de dois dos seus ângulos, na intersecção do qual se encontra o centro do círculo circunscrito. O raio é a distância do ponto de interseção das bisecetas ao vértice de qualquer canto do polígono. O centro do círculo inscrito encontra-se na interseção de perpendiculares construídas dentro do polígono dos centros dos lados (essas perpendiculares são chamadas de intermediárias). É suficiente construir duas dessas perpendiculares. O raio do círculo inscrito é igual à distância do ponto de interseção das perpendiculares medianas ao lado do polígono.
Dica 4: Como encontrar o raio de um círculo
Definição do raio círculos é uma das principais tarefas da matemática. Existem muitas fórmulas para contabilidade do raio, basta saber apenas alguns parâmetros padrão. Graficamente, o raio é denotado pela letra R do alfabeto latino.

Instruções
1
Um círculo é uma curva fechada. Os pontos em seu plano são equidistantes do centro, que se situa no mesmo plano juntamente com a curva. Raio - segmento círculos, conectando seu centro com qualquer um dos seus pontos. Com sua ajuda, você pode aprender muitos outros parâmetros da figura, então é um parâmetro chave. O valor numérico do raio será o comprimento deste segmento.
2
Além disso, é necessário distinguir o raio de uma figura do seu diâmetro (o diâmetro conecta dois pontos tão distantes quanto possível um do outro). Para usar o método matemático de encontrar do raio você precisa saber o comprimento ou o diâmetro círculos. No primeiro caso, a fórmula parecerá "R = L / 2?", Onde L é o comprimento conhecido círculos, e o número? é igual a 3,14 e é usado para denotar um certo número irracional.
3
No caso em que apenas o diâmetro é conhecido, a fórmula parecerá "R = D / 2".
4
Se o comprimento círculos Desconhecido, mas há dados sobre comprimento e alturade um certo segmento, então a fórmula terá a forma "R = (h ^ 2 * 4 + L ^ 2) / 8 * h", onde h é a altura do segmento (é a distância do meio da corda para a parte mais saliente do arco) comprimento do segmento (que não é o comprimento da corda). Chord é um segmento de linha que conecta dois pontos círculos.
Dica 5: como encontrar a velocidade instantânea
Para encontrar instantâneo velocidade em um movimento uniforme, divida a distância percorrida pelo corpo, pelo tempo para o qual foi superado. Se houver movimento irregular, descubra o valor e a contagem de aceleração velocidade em cada momento do tempo. Em uma queda livre, o instantâneo velocidade depende da aceleração da queda e do tempo livres. Instantâneo velocidade pode ser medido com um velocímetro ou radar.

Você precisará
- Para determinar a velocidade instantânea, tome um radar, um velocímetro, um cronômetro, uma fita métrica ou um buscador de alcance, um acelerômetro.
Instruções
1
Determinação da velocidade instantânea no uniformeSe o corpo se move de forma uniforme, mida a distância em metros em uma roleta ou buscador de faixa, então divida o valor obtido pelo intervalo de tempo em segundos para o qual esse segmento foi passado. Meça o tempo com um cronômetro. Então ache a média velocidade, dividindo o comprimento do caminho pelo tempo que passa (v = S / t). E como o movimento é uniforme, a média velocidade será igual à velocidade instantânea.
2
Determinação da velocidade instantânea em não-uniformeO principal tipo de movimento não uniforme é o movimento uniformemente acelerado. Usando um acelerômetro ou qualquer outro método, mede o valor da aceleração. Depois disso, conhecer a inicial velocidade movimento, adicione a ele o produto da aceleraçãoe o tempo durante o qual o corpo está em movimento. O resultado é a velocidade instantânea em um determinado momento. (v = v0 + a • t). Ao calcular, observe que se o corpo diminui sua velocidade (inibe), o valor de aceleração será negativo. Se o movimento começar de um estado de repouso, a inicial velocidade é igual a zero.
3
Determinação da velocidade instantânea com livrePara determinar a velocidade instantânea de um corpo que cai livremente, o tempo de queda deve ser multiplicado pela aceleração devida à gravidade (9.81 m / s²) e o cálculo deve ser feito com a fórmula v = g • t. Por favor note que com queda livre, a inicial velocidade O corpo é zero. Se o corpo cai de uma certa altura, então, para determinar a velocidade instantânea no momento da queda dessa altura, multiplique seu valor em metros pelo número 19.62 e, a partir do número resultante, extraia a raiz quadrada.
4
Determinação da velocidade instantânea com um velocímetro ou radar Se o corpo em movimento estiver equipado com um velocímetro (carro), sua escala ou painel de avaliação eletrônico exibirá continuamente uma imagem instantânea velocidade em um determinado momento. Ao observar o corpo a partir de um ponto fixo (terra), aponte o sinal do radar para ele, o display exibirá uma imagem instantânea velocidade corpo em um determinado momento.
Dica 6: como determinar o raio da curvatura
Para estudar o movimento de algum físicoobjeto (carro, ciclista, bola na roleta) é suficiente para estudar o movimento de alguns de seus pontos. Ao estudar o movimento, verifica-se que todos os pontos descrevem algumas linhas curvas.

Instruções
1
Saiba que as curvas podem descrever o movimentolíquido, gás, raios de luz, racionalizações. O raio de curvatura para uma curva plana em um determinado ponto é o raio do círculo tangente neste ponto. Em alguns casos, a curva é dada por equações, e o raio de curvatura é calculado pelas fórmulas. Consequentemente, para determinar o raio de curvatura, é necessário conhecer o raio de um círculo tangente a um determinado ponto.
2
Determine o ponto A no plano da curva, pegue outro ponto B. Desenhe as tangentes à curva existente que passa pelos pontos A e B.
3
Passe pelas linhas dos pontos A e B,Perpendicular à tangente construída, estenda-os até a intersecção. Designe o ponto de interseção das perpendiculares como 0. O ponto O é o centro do círculo tangente em um determinado ponto. Daí o OA é o raio do círculo, isto é, curvatura em um determinado ponto particular A.
4
Observe que quando um ponto se move ao longo de qualquer trajetória curvilínea em qualquer momento de movimento, ele se move ao longo de um círculo que varia de ponto a ponto.
5
Se por um ponto no espaço determinar as curvaturasem duas direções mutuamente perpendiculares, então essas curvaturas serão chamadas de principal. A direção das curvaturas principais deve ser necessariamente 900. Para os cálculos, a curvatura média é freqüentemente igual à metade da soma das curvaturas principais, e a curvatura gaussiana é igual ao seu produto. Há também o conceito de curvatura de uma curva. Este é o recíproco do raio de curvatura.
6
A aceleração é um fator importante no movimento do ponto. A curvatura da trajetória afeta diretamente a aceleração. A aceleração ocorre quando um ponto com velocidade constante começa a se mover ao longo de uma curva. Não só a magnitude absoluta da velocidade altera, mas também sua direção, há uma aceleração centrípeta. Ou seja. na realidade, o ponto começa a se mover ao longo do círculo, que toca em um determinado momento no tempo.
Dica 7: como encontrar a aceleração normal
A aceleração normal é observada no caso,quando o corpo se move ao longo da circunferência. E este movimento pode ser uniforme. A natureza dessa aceleração está relacionada ao fato de que o corpo que se move ao longo do círculo muda constantemente a direção da velocidade, uma vez que a velocidade linear é tangencial a cada ponto do círculo.

Você precisará
- velocímetro ou radar, cronômetro, localizador de alcance.
Instruções
1
Usando um velocímetro ou radar, mede o linearvelocidade do corpo que se move ao longo da circunferência. No intervalo, mede seu raio. Para encontrar a aceleração normal de um corpo que se move ao longo de um círculo, tome o valor da velocidade em um determinado momento, acerte-o e divida pelo raio do círculo do caminho do movimento: a = v² / R.
2
Se a velocidade angular do corpo é conhecida durante o movimento,encontre a aceleração normal usando seu valor. Para fazer isso, acalme a velocidade angular e divida pelo raio do círculo ao longo do qual o corpo se move: a = ω² • R. Se não for possível medir a velocidade de um corpo movendo-se ao longo de um círculo, calcule-o pelo período de rotação. Para encontrar o período de rotação, use o cronômetro para medir o tempo para o qual o corpo retorna ao ponto de partida. Se o corpo se mover muito rápido, espere o tempo durante o qual são feitas várias revoluções de corpo inteiro. O tempo resultante é dividido pelo número de rotações e você obtém o tempo de uma rotação, chamado período de rotação. O tempo é medido em segundos. Para encontrar a aceleração normal, divida o número 6.28 pelo período de rotação do corpo. O número resultante é quadrado e multiplicado pelo raio do círculo ao longo do qual o corpo se move: a = (6.28 / T) ² • R.
3
A aceleração normal pode ser medida sabendo a frequênciarotação do corpo. Para calcular a frequência, divida um número de rotações pelo tempo em segundos, para o qual elas ocorrem. O resultado é o número de rotações por segundo - esta é a frequência. Calcule a aceleração normal do corpo, multiplicando o número 6.28 pela freqüência de rotação, o número resultante é quadrado. Multiplique o resultado pelo raio do círculo ao longo do qual o corpo se move: a = (6.28 • υ) ² • R.
Dica 8: Como encontrar o raio da curvatura
Seja dada uma função definida pela equação y =f (x) e o gráfico correspondente. É necessário encontrar o raio de sua curvatura, isto é, medir o grau de curvatura do gráfico desta função em algum ponto x0.

Instruções
1
A curvatura de qualquer linha é determinada pela velocidaderotação de sua tangente no ponto x quando este ponto se move ao longo da curva. Uma vez que a tangente do ângulo tangente é igual ao valor da derivada de f (x) neste ponto, a taxa de mudança desse ângulo deve depender da segunda derivada.
2
O padrão de curvatura é lógico para aceitar um círculo,Uma vez que é uniformemente curvo em todo o seu comprimento. O raio de tal círculo é a medida da sua curvatura. Por analogia, o raio de curvatura de uma determinada linha no ponto x0 é o raio do círculo, que mede com precisão o grau de sua curvatura neste ponto.
3
O círculo necessário deve estar em contato comcurva dada no ponto x0, isto é, estar localizada no lado de sua concavidade, de modo que a tangente à curva neste ponto também seja tangente ao círculo. Isso significa que se F (x) é uma equação de um círculo, as seguintes igualizações devem ser seguras: F (x0) = f (x0), F '(x0) = f' (x0). Esses círculos, obviamente, existem infinitamente. Mas, para medir a curvatura, é necessário escolher o que mais corresponde à curva dada neste momento. Uma vez que a curvatura é medida pela segunda derivada, é necessário adicionar a estas duas equações uma terceira: F '' (x0) = f '' (x0).
4
A partir dessas relações, o raio de curvatura é calculado pela fórmula: R = ((1 + f '(x0) ^ 2) ^ (3/2)) / (| f "(x0) |). O inverso do raio de curvatura, é chamado de curvatura da linha em um determinado ponto.
5
Se f (x0) = 0, então o raio de curvatura éinfinito, ou seja, a linha neste ponto não é curvada. Isso sempre é verdade para linhas retas, bem como para qualquer linha em pontos de inflexão. A curvatura em tais pontos, respectivamente, é zero.
6
O centro do círculo que mede a curvatura da linha em um determinado ponto é chamado de centro de curvatura. Uma linha que é um locus geométrico para todos os centros de curvatura de uma determinada linha é chamada de evolução.
Dica 9: Como encontrar a aceleração centrípeta
A aceleração centrípeta ocorre quandoo movimento do corpo ao longo da circunferência. É direcionado ao seu centro, medido em m / s². Uma característica deste tipo de aceleração é que existe mesmo quando o corpo se move a uma velocidade constante. Depende do raio do círculo e da velocidade linear do corpo.

Você precisará
- - Velocímetro;
- - um dispositivo para medir a distância;
- - Cronômetro.
Instruções
1
Para encontrar o centrípetaaceleração, mede a velocidade de um corpo movendo-se ao longo de um caminho circular. Você pode fazê-lo com um velocímetro. Se isso não for possível, calcule a velocidade da linha. Para fazer isso, observe o tempo gasto para uma revolução completa ao longo de um caminho circular.
2
Esse tempo é o período de rotação. Expresse isso em segundos. Meça o raio do círculo ao longo do qual o corpo se move com uma régua, uma fita métrica ou um aparelho de controle de laser em metros. Para encontrar a velocidade, encontre o produto do número 2 pelo número π≈3,14 e o raio R do círculo e divida o resultado pelo período T. Essa será a velocidade linear do corpo v = 2 ∙ π ∙ R / T.
3
Encontre a aceleração centrípeta a, dividindoo quadrado da velocidade linear v pelo raio do círculo ao longo do qual o corpo R (ay = v2 / R) se move. Usando as fórmulas para determinar a velocidade angular, a frequência e o período de rotação, encontre este valor usando outras fórmulas.
4
Se a velocidade angular ω for conhecida e o raio(a circunferência ao longo da qual o corpo se move) R então a aceleração centrípeta será igual a az = ω2 ∙ R. Quando o período de rotação do corpo T é conhecido e o raio da trajetória R, então ac = 4 ∙ π² ∙ R / T². Se a frequência de rotação ν (o número de rotações completas por segundo) é conhecida, determine a aceleração centrípeta de acordo com a fórmula az = 4 ∙ π² ∙ R ∙ ν².
5
Exemplo: O carro, cujo raio de rodas é de 20 cm, se move ao longo da estrada a uma velocidade de 72 km / h. Determine a aceleração centrípeta dos pontos extremos de suas rodas. Solução: A velocidade linear dos pontos de qualquer roda é de 72 km / h = 20 m / s. Gire o raio da roda em metros R = 0,2 m. Calcule a aceleração centrípeta, substituindo os dados resultantes na fórmula az = v² / R. Obter az = 20² / 0,2 = 2000 m / s². Esta aceleração centrípeta com movimento rectilíneo uniforme será nos pontos extremos das quatro rodas do carro.
Dica 10: Como encontrar a aceleração tangencial
Tangencial aceleração ocorre em corpos movendo-se ao longo de um curvilíneotrajetória. É direcionado na direção de mudar a velocidade do corpo ao longo da tangente à trajetória do movimento. A aceleração tangencial não ocorre em corpos que se movem uniformemente ao longo da circunferência, eles têm apenas uma aceleração centrípeta.

Você precisará
- - velocímetro ou radar;
- - régua ou fita métrica;
- - Cronômetro.
Instruções
1
Encontre a aceleração tangencial a si seEle sabe ponto de aceleração total movendo ao longo de um caminho curvo e sua aceleração centrípeta de um. Para esta finalidade, o quadrado da aceleração centrípeta quadrado cheio aceleração subtrair, e o valor obtido do extracto de raiz quadrada aτ = √ (a²-an²). Quando a aceleração centrípeta é desconhecido, mas não é a velocidade instantânea, uma régua ou fita medir o raio de curvatura do percurso e localizar o seu valor dividindo o quadrado da instantânea velocidade v, que medem o velocímetro radar ou sobre o raio de curvatura da trajectória R, um = V² / R.
2
Um exemplo. O corpo move-se ao longo de um círculo com um raio de 0,12 m. Sua aceleração total é de 5 m / s², determina a sua aceleração tangencial, no momento em que a velocidade é de 0,6 m / s. Primeiro, encontre a aceleração centrípeta do corpo à velocidade especificada, para isso, divida seu quadrado pelo raio da trajetória an = v² / R = 0,6² / 0,12 = 3 m / s². Encontre a aceleração tangencial pela fórmula aτ = √ (a²-an²) = √ (5²-3²) = √ (25-9) = √16 = 4 m / s².
3
Determine a quantidade de aceleração tangencialatravés da mudança no módulo de velocidade. Para fazer isso, use o velocímetro ou o radar para determinar a velocidade inicial e final do corpo por um certo período de tempo, que você mede com a ajuda de um cronômetro. Encontre a aceleração tangencial subtraindo o valor inicial da velocidade v0 do v final e dividindo-o pelo intervalo de tempo t, durante o qual ocorreu esta alteração: aτ = (v-v0) / t. Se o valor da aceleração tangencial for negativo, o corpo diminui, se positivo - acelera.
4
Um exemplo. Durante 4 s, a velocidade do corpo que se move ao longo da circunferência diminuiu de 6 para 4 m / s. Determine sua aceleração tangencial. Aplicando a fórmula de cálculo, obtenha aτ = (v-v0) / t = (4-6) / 4 = -0,5 m / s². Isso significa que o corpo diminui com uma aceleração cujo valor absoluto é de 0,5 m / s².
Dica 11: Qual é o raio de curvatura da lente?
O raio de curvatura das lentes de contato é um parâmetro,que determina seu tamanho. Se for levado incorretamente, ao usar essas lentes, uma pessoa experimentará inconvenientes e sua visão pode se deteriorar significativamente.

Como é o raio de curvatura da lente?
O raio de curvatura da lente dependerá da estruturaglobos oculares humanos. Uma vez que a lente é colocada na córnea do olho, ela deve repetir a forma com a maior precisão possível. O globo ocular humano tem aproximadamente os seguintes parâmetros: o comprimento do equador do olho (o maior círculo do olho no plano frontal) é de 23,6 mm, o comprimento do eixo óptico é de 24 mm, o diâmetro vertical do olho é de 23,4 mm. Em uma pessoa que tenha tais parâmetros padrão, o raio de curvatura será de 8,6. As lentes com taxas de 8,3 a 8,8 podem ser facilmente encontradas à venda. Se o raio de curvatura se desviar significativamente da estatística média, as lentes devem ser feitas por encomenda. O seu esboço é feito em consulta com um oftalmologista. O médico determina o desejado raio de curvatura da lente de uma forma chamada "autorefractometria". O especialista examina a córnea do olho usando métodos de diagnóstico por computador. O princípio da emissão de luz infravermelha é a base da autorefractometria. A imagem resultante do feixe de luz antes dele é refletida a partir da retina e depois é fixada por sensores especiais. Além do raio de curvatura da lente, também é determinada a diferença de refração (a força de refração do sistema óptico do olho expresso em dioptreras) entre os olhos e a magnitude do astigmatismo (a incapacidade dos olhos para focar adequadamente a visão). Como ponto de fixação, o estudo usa uma imagem infinitamente distante.E se as lentes de contato não se encaixam
Caso as lentes já tenham sido compradas e o raioA curvatura não é assim, você precisa proceder da seguinte maneira. Se essa diferença não exceder 0,2, os médicos normalmente aconselham usar tais lentes, desde que não se sinta desconforto. Se esse desvio for superior a 0,2, eles não podem ser usados. No caso de uma pessoa usar lentes de contato mais convexas, sua mobilidade será difícil. Os vasos sanguíneos serão espremidos, isso inevitavelmente levará a vermelhidão dos olhos. Os globos oculares estarão em tensão constante, pode haver distúrbios na lacrimejamento. A ameaça de inflamação aumentará, a visão será instável. No caso de o raio de curvatura ser maior do que o índice requerido, as lentes de contato serão muito móveis. Eles podem facilmente cair dos olhos, danificar a córnea, causar lágrimas. As lentes planas se afastam facilmente da córnea, uma pessoa não consegue ver nada. Como eles machucam os músculos superiores dos olhos, quando aparecerá uma dor piscando.Dica 12: Como Eratóstenes calculou o raio da Terra
O lendário astrônomo e matemático grego antigoErastofen determinou experimentalmente o ângulo da inclinação do Sol para a Terra em duas cidades, que, em sua opinião, estão em um dos meridianos. Sabendo a distância entre eles, ele calculou matematicamente o raio do nosso planeta. Os cálculos revelaram-se bastante precisos.

O método de Erastofen
Erastofen viveu na cidade de Alexandria,no norte do Egito, perto da foz do rio Nilo, na costa do Mediterrâneo. Ele sabia que em um certo dia de cada ano na cidade de Siena, no sul do Egito, no fundo dos poços, não havia sol. Ou seja, o Sol nesse momento está diretamente acima da cabeça. No entanto, em Alexandria, localizada ao norte de Siena, mesmo no dia do solstício de verão, o Sol nunca está diretamente em cima. Erastofen percebeu que é possível determinar até que ponto o Sol é deslocado da posição "diretamente acima da cabeça" medindo o ângulo formado pela sombra do objeto vertical. Ele mediu o comprimento da sombra da torre alta em Alexandria e, usando a geometria, calculou o ângulo entre a sombra e a torre vertical. Acabou sendo cerca de 7,2 graus, e Erastofen usou construções geométricas mais complexas. Suponhamos que o ângulo da sombra seja exatamente o mesmo que entre Alexandria e Siena, se você contar a partir do centro da Terra. Por conveniência, descobri que 7,2 graus é 1/50 de um círculo completo. Para encontrar a circunferência da Terra, a distância entre Siena e Alexandria foi multiplicada por 50. Segundo Erastofen, a distância entre as cidades era de 5 mil estágios. Mas não havia uma unidade geral de comprimento naqueles primeiros tempos, e hoje não se sabe em qual estágio Erastofen foi usado. Se ele aplicou o egípcio, que era de 157,5 m, o raio da Terra era de 6287 km. O erro neste caso foi de 1,6%. E se você usou o estágio grego mais comum, igual a 185 m, o erro seria de 16,3%. Em qualquer caso, a precisão dos cálculos é muito boa para esse tempo.Biografia e atividade científica de Erastofen
Acredita-se que Erastofen nasceu em 276 aAD na cidade de Cirene, que ficava no território da moderna Líbia. Ele estudou por vários anos em Atenas. Ele passou uma parte considerável de sua vida adulta em Alexandria. Ele morreu em 194 aC com a idade de 82 anos. Segundo algumas versões, ele mesmo morreu de fome depois de ser cego. Durante muito tempo Erastofen dirigiu a Biblioteca de Alexandria, a biblioteca mais famosa do mundo antigo. Além do fato de que ele calculou o tamanho do nosso planeta, ele fez uma série de importantes invenções e descobertas. Inventou um método simples para determinar números primos, agora chamado de "peneira de Erastofen". Ele desenhou um "mapa do mundo", no qual mostrava todas as partes do mundo, conhecidas naquela época pelos antigos gregos. O cartão foi considerado um dos melhores para o seu tempo. Desenvolveu um sistema de longitude e latitude e um calendário que incluiu anos bissextos. Inventou a esfera armilar, um dispositivo mecânico usado pelos primeiros astrônomos para demonstrar e prever o movimento visível das estrelas no céu. Também fez um catálogo de estrelas, que incluiu 675 estrelas.O cientista grego Eratosthenes Kirensky pela primeira vez no mundo calculou o raio da Terra Cálculo de Eratóstenes da Circunferência da Terra Eratóstenes